|
|
||||||||||||||||
|
|
||||||||
|
|
||||||||
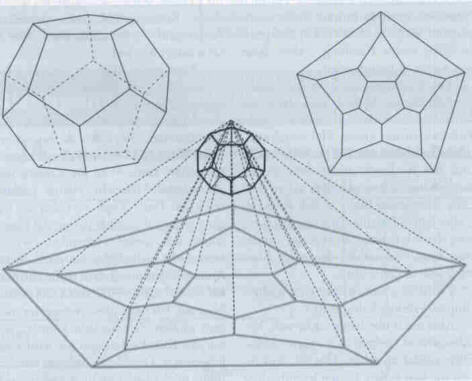
So macht man einem R2-Menschen ein Dodekaeder (links) begreiflich:
Man setzt ein Drahtmodell auf die Ebene und hängt eine punktförmige Lichtquelle dicht über seine Deckfläche (Mitte). Der Schatten des Drahtmodells in der Ebene ist das Schlegel-Diagramm (rechts):
Drei regelmäßige Fünfecke Drei regelmäßige Fünfecke in der Ebene lassen eine Lücke, die durch Falten entlang der gemeinsdamen Kanten geschlossen wird (links).
Entsprechend schließt man im vierdimensionalen Raum die Lücke zwischen drei Dodekaedern, indem man sie gegeneinander faltet - entlang der gemeinsamen Ebenen.
Die Projektion des 120-Zells in den R3.
Die 120 Dodekaeder erscheinen in neun Schichten: zumindest das Baby (Mitte), klein, weiß und unverzerrt, darum der Reihe nach 12 blaue, 20 rote, 12 gelbe, 30 grüne, 12 gelbe, 20 rote und 12
blaue Dodekaeder, die immer größer und verzerrter werden (alle Dodekaeder einer Schicht sind kongruent). Das alles umschließende weiße Dodekaeder, der Käfig (oben), ist wieder unverzerrt.
Die Zentralprojektion eines 24-Zells im Kantenmodell
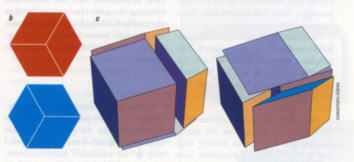
Ein Würfel auf die Spitze gestellt (a) und von oben mit parallelem
Licht beschienen, wirft als Schattenin den R2 (die Ebene) ein doppeltes Sechseck (b). Entsprechend werden aus einem vierdimensionalen Würfel durch Zentralprojektion in den R3 zwei Rhombendodekaeder (c), die dasselbe Volumen einnehmen und nur an dessen Oberfläche
miteinander Kontakt haben (hier sind deren Komponenten, die Rhoboeder, zur Verdeutlichung etwas auseinander verschoben). Die Projektionen sind so gewählt, dass im Projektionsbild wie im Original alle Kanten gleich lang sind.
Die Parallelprojektion des (6,6)-Biprismachors füllt ein räumliches Volumen doppelt. Hier gezeigt ist eine der beiden Füllungen; sie enthält jeweils die
Hälfte der beiden Sechserringe sechsseitiger Prismen, die sich umeinander winden.
Autor:
Christoph Pöppe, promovierter Mathematiker und Redakteur bei Spektrum der Wissenschaft. Weblinks zu diesem Thema:
|
||
Contact email@raum-und-zeidimensionen.de with comments or questions regarding this site. |